


For you and me, an object like a tennis ball or a car can never be said to be moving directly away from you and directly towards you at the same time. That wouldn't make any sense to us; it has to be either one or the other. But for a computer, cell phone, robot or drone that uses the Grassland software client as its perception and imagination this is exactly how the world appears. And it's not just that an object moves directly towards them and directly away from them at the same time, it moves in all directions at once.
The reason why is because Grassland lets these machines see the world from a completely propagated (decentralised, spread out) frame-of-reference (perspective). Why? Because the universe is also a completely propagated frame-of-reference. There is no central location in space, a scientific fact that can be as disturbing to people today as the fact that their planet isn't even in the center of its own solar system was to people in the Middle Ages. Which means that a point of view that sees you move in all directions at once isn't wrong at all. In fact, it is much more correct than your own because it's imitating the universe itself. Which means that it's you and I who are the ones who can't see the world how it really is, the way in which reality would make the most sense.
This article is going to be short, illustrated and oversimplified in order to make things easier. I tried to keep parts 2, 3 and 4 below as close as possible to something that even a 5 year old could understand. While the last half is more on the level of someone age 20 and up. But hopefully it'll give you a better understanding of Grassland's mathematics, the motion of objects (mechanics) and its theory governing space and time, matter and energy.
It won't have the same elegance and clarity that is in the full paper. Which couldn't be adequately explained on the site's original front page, but which I had promised to provide in a follow-up supplement. So I hope this will give you some idea about the things that this technology now makes possible. Which are being added to the "full node" version of the Grassland software client. This will only cover a tiny bit of Section 1 (geometry) and a tiny bit of Section 4 (physics/mechanics), out of eight sections in the complete paper.
Of course, most of you aren't five years old. But history's best mathematicians have always attributed their success to having a stronger and much more adaptable imagination than their peers. So it's likely that the only way to wrap your head around Grassland mathematics is to read this like you really are five years old.

Fig. 4: That horizon is preserved no matter how much you move or rotate either your fist or yourself. It's an inescapable property because of the fixed nature of your perspective.
First, curl your hand into a fist. Notice that you can only see one side of it at a time. And that your fist always has an edge in all directions. A type of border that you can't see beyond. We'll call this edge a horizon.
All objects have these horizons to you. The surface of everything you see also has this border that you can't see beyond. And it never changes from your perspective. It's there no matter how much you rotate, flip or move your fist or your head. Mathematicians call a feature that doesn't change under transformation an invariant (remember that word).
Even if you could take out one of your eyes and hold it on the other side of your fist, all the other objects in the room would still have these horizons. In fact, you'd see even less of those other objects because in order to point both eyes at your fist you'd have to point them in opposite directions. And your brain would also have to be able to adjust in order to make sense of an eye that isn't where it's supposed to be. To overcome this problem you would need a very adaptable brain. One that could make sense of two eyes at unusual distances from one another.
But in order to remove all horizons as far as you can see you'd need something more. A brain that can make sense of signals from an infinite number of "eyes". If you possessed a brain like that, you'd be able see the entire surface of your fist in the same way that you can see the surface of the back of your hand when you spread it out in front of you. The entire surface would be turned towards your perspective.
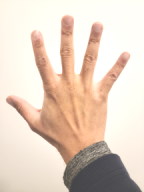
Fig. 5: Spreading out your hand is the only way to visualize the geometric transformaion that I'm talking about in a way that makes the most sense to your eyes. An inverted panorama would not only still have edges, it would warp distances. (This is why mathematicians use algebraic equations, functions, etc. It's the only language that allows us to completely explain things like this that just can't be fully described or understood in any other way.)
Remember that what I'm describing here isn't a change of the object itself. Your hand would still be in the shape of a fist. But it would appear to this other type of observer as if all sides of your fist are turned towards their frame-of-reference (Like Fig. 5). But that's because all sides are turned towards their frame-of-reference. And although your fist still has a surface to this observer it no longer has any "edges" or horizons.
But right now, no matter where you look, everything you see has a surface that curves away from you. And that's because there is something about your frame-of-reference that doesn't change. Something that is invariant under all the transformations that the laws of physics has made available to you. And although you and this other more "artificial" observer could be viewing the same object, some very basic and fundamental properties of nature would look very different to each of you. So the type of transformations we talk about with Grassland geometry have to do with something much more fundamental...
But in order to explain it there's something else that I need to explain first. What geometry actually is. It isn't quite what they teach you in primary or secondary school. Which is why I'm using the word in a way you're probably not use to.
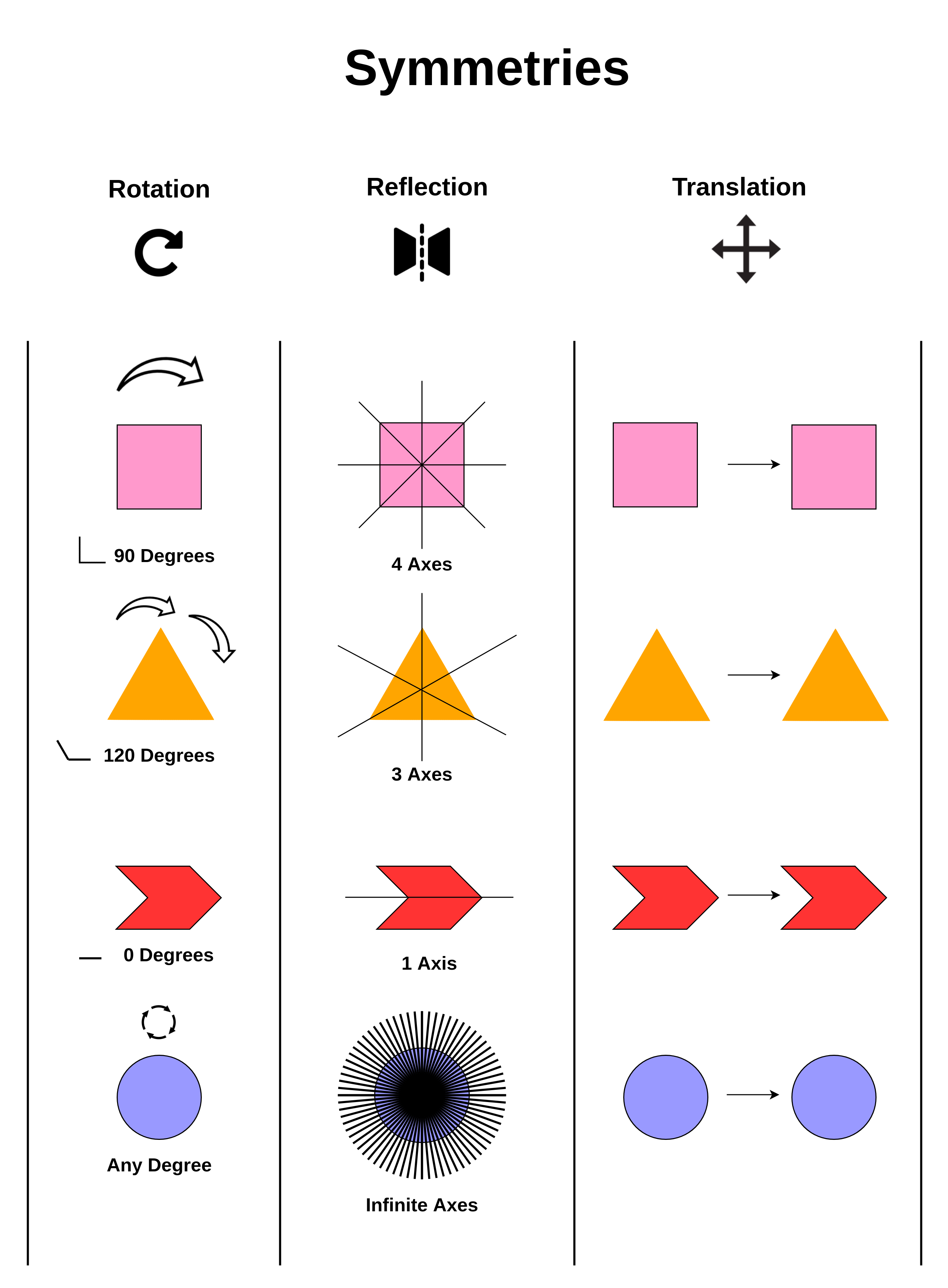
Fig. 6: Rotation: A square rotated 90 degrees looks the same. And an equilateral triangle rotated 120 degrees looks the same. But you can't rotate a chevron in any way that has symmetry. But you can rotate a circle any amount you want. Reflection: All four objects have at least one axis of symmetry that they can be flipped over. Translation: All four objects look the same if all their points are moved in the same direction. These rigid body transformations that don't deform the shape are from Euclidean geometry.
Geometry isn't really a way of measuring things like the properties (distances, points, lines, curves, angles etc.) of shapes like squares, circles, triangles etc. Well it is, but not in the way you think it is. Mathematicians define geometry as a study of every possible type of transformation you could perform on those shapes. Rotations, reflections, translations (moving), stretching, shearing, etc. etc.
And they group these transformations as different types of geometries (Euclidean, hyperbolic, affine, etc.). And what separates one geometry from another is which of those properties don't change, are invariant, when a transformation is performed. For example, no matter how you rotate or move a circle it looks exactly like the same circle because distances and angles are invariant after (Euclidean) rotations, translations or reflections. But if you bend a square's corners to make a diamond shape, distances and angles aren't preserved because they're not concepts of affine geometry. But points, lines and planes are concepts of affine geometry because they don't change.
And when a transformation doesn't change a particular property of a shape, we call this a symmetry. Because those properties look the same on either side (before and after) of the transformation. So from here on, think of geometry as a bunch of geometries. Where each of them are a set of property perserving transformations.
Now, what all these geometries take for granted is the concept of a single frame-of-reference or scope. In physics, this is also called an observer.
And that way of thinking appears to be the most natural. Since it seems to be how we and certainly any intelligent creature must observe the universe. One observer to one frame-of-reference is an unwritten rule mathematicians and as a result, physicists take for granted. We don't question the assumption that a completely different frame-of-reference must be a completely different observer.
So there are some basic things that separate Grassland geometries from the much more natural geometries that people have been discovering/inventing since the ancient Egyptians and Greeks up to the present day. Two of them are...
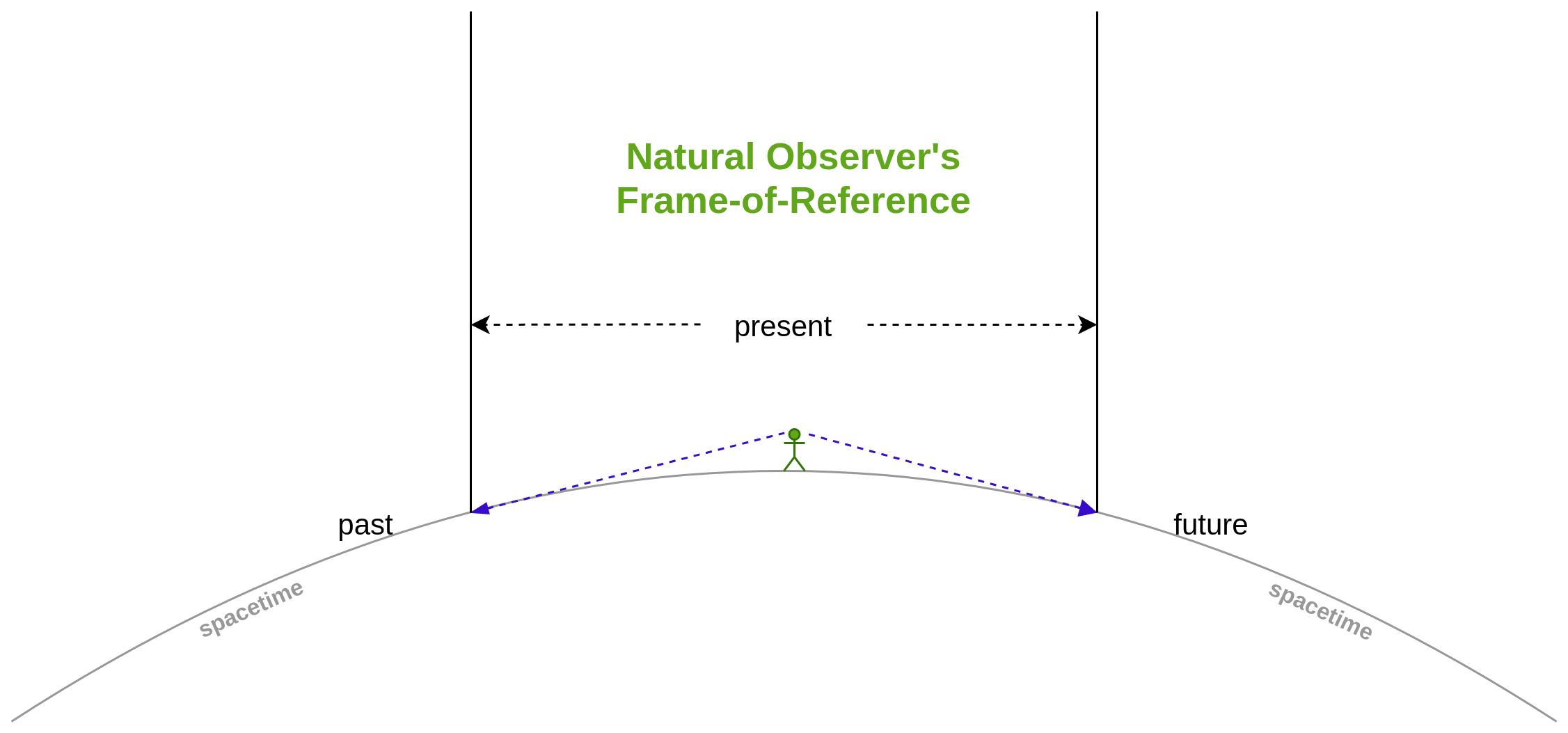
Fig. 7: The two blue lines of sight mark the upper limits or horizon of the observer's frame-of-reference in spacetime. Just like the horizon for anyone on a planet's surface is a measure of how far you can see from your location and it is determined by the curvature of the planet, the present for any observer is determined by the curvature of spacetime at their location. The scale of this diagram is exaggerated for illustrative purposes.
Einstein's theory of relativity tells us that matter and energy cause space and time, collectively referred to as spacetime, to more or less curve away from any frame-of-reference his observers could be in. Like the fist we discussed in the previous section. (At this point, reading this as if you were five and adapting to a completely different way of thinking is going to come in handy). Believe it or not, this curvature of spacetime is what causes the experience of gravity that keeps you from floating into space.
This curvature is also why you only experience a narrow band of time known as the present. That's because spacetime's curvature causes the past and the future to curve away from you in both directions. The past and the future always sit below the horizon, constantly pushed beyond the perspective of observers in Einstein's universe. As in the the figure above.
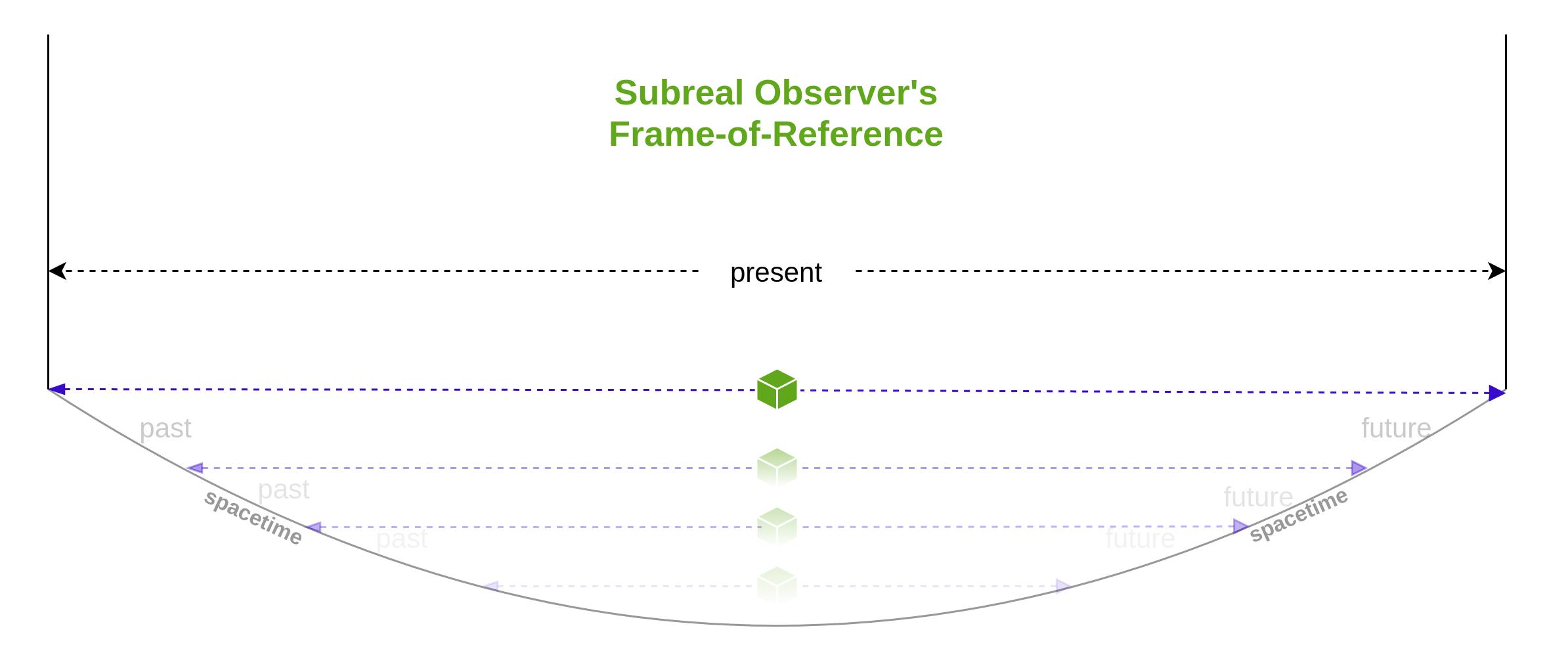
Fig. 8: The present according to a subreal observer. Notice that if you were to draw a straight, horizontal line directly underneath the natural observer in the previous figure, just touching the spacetime curve, it forms what's called a tangent line, which is a straight line that just touches the edge of a curved one. And you'll see that you can regard this subreal observer as simply a natural observer that has been reflected over the tangent to curved spacetime. And this is similar to what I said about the fist above. Since spacetime doesn't change under the transformations of Grassland geometry, just the observer's orientation to it.
But for our universe, I defined a new type of observer. An extremely artificial one. One for whom light is curved towards its frame-of-reference because spacetime itself is curved towards its frame-of-reference. As the result of an equivalent type of transformation. One that causes the scope of what this observer defines as being the present to be a changing variable rather than a fixed constant.
Meaning temporal horizons aren't concepts under any theory based on Grassland geometry since even the past and the future curve towards its observers. In the Grassland client, this "block universe" of an ever expanding spacetime present is encoded as its distributed blockchain (No pun intended; it's just a coincidence). And its distributed indexing system uses an extendable binary address length. Which gives it enough numerical combinations to uniquely reference every possible object-event within a ~15 billion kilometres range (roughly to the outer edge of the Kuiper asteroid belt) over the next ~400 years. This design provides an arbitrary level of precision. Which allows machines to consume resources in a manner that becomes physically reversible because it becomes logically reversible (see next section).
Moreover, the transformations that cause both the surface of a fist and the surface of spacetime itself to curve away or towards an observer are equivalent under our new mechanics. They are two sides of an even more fundamental transformation. From which we can not only derive the three postulates (see the "short paper" that was the original home page) that govern the theorem of the software client itself, but it also gives us a useful definition for the natural experiences of distance and duration. Explaining what they are from a more fundamental context.
Now, there's quite a lot more to say about Grassland's "equivalence principle" and what actually predicts this subreal curvature. But that's well outside the scope of this article.
And now the 'analytics' (coordinate system) of this geometry and the 'analysis' (calculus) built on top of it provide us with a very different and better way of describing and modelling these three phenomena. One that's as powerful and efficient as it is unconventional, doing for us what the Cartesian plane did for Euclidean geometry and what Newton's and Leibniz's Calculus (the one you learn in school) did for curvature. And it lets the elements of this propagated system reach consensus on the set of property preserving transformations that define what the physics of the universe that they communicate to each other must necessarily be. Which they can reach without the need for any natural intelligence (e.g. physicist, mythological deity, etc.) to have defined it for them.
Moreover, the usefulness and flexibility of this math also allows machines to efficiently and autonomously solve classes of problems that had never even been considered before, let alone undertaken. Most of which are also outside the scope of this article. But one of them is so essential to our main purpose here that it cannot be overemphasized...
Fig. 2b: There is a very important type of reversible transformation in math called the general linear group. It defines a particular set of numerical values that can be reversed repeatedly in such a way that they produce new values. It is sometimes denoted by its abbreviation, 'GLn'.
Machines that "...consume resources in a manner that becomes physically reversible since it becomes logically reversible" is related to a complex subject that computer scientists call reversible computing. But I'm going to put it in very practical terms.
Every machine, of course, exists as a solution to some problem or another. But machines use up energy, cause pollution and change their environments. And they make mistakes, either because they're in a new environment or just through simple ignorance. But Grassland gives machines an undo button for the entire physical universe that they perceive because it scales to remember where everything was and what everything and everyone was doing at every single point in time. Like remembering the order of moves in a game of Go (Weiqi).
Which means that anything that is a part of Grassland's universe is physically reversible by definition. This is an important distinction because it means that machines can rewind their universe as many times as they need to until they've figured out a solution to nearly any problem. And because both the mistakes and the successful actions that they perform are also saved in Grassland that means every other machine can now "remember" the best way to solve that problem too. Therefore, allowing anything measured with this geometry to be transferred across large distances and durations.

Fig. 9: Go (Weiqi) is an ancient and very popular Chinese board game. It's kind of like chess except there are no kings, you start with nothing and everything about it is decentralised. Success is achieved by capturing as much territory as possible by creating as many "eyes" as possible while using the fewest number of resources.
If you reread those last two paragraphs, replacing "machine" with "human" (or "animal") wherever you'd like, you'll understand the future and the past that Grassland is creating. One that allows computers, cell phones, robots, drones, etc. to jump across time and space millions of times per second in order to figure out how to solve real world problems; in the same way that modern AI's quickly learn how to beat grandmaster Go (Weiqi) players by internally playing and recalling millions of virtual games per second. Likewise, Grassland lets your machines acquire multiple lifetimes worth of real world experience in whatever they need within a few moments of them being turned on.
And now you also understand why this ELI5 couldn't be made much simpler without sounding insane. I couldn't just say "I built a time machine out of a Raspberry Pi so robots could travel through parallel universes". No matter how true that may be.
Differences of Scale: When the relative scope of Grassland transformations is less eccentric and more conventional, an observer performing experiments won't see much of a difference between the predictions made under a theory based on Grassland geometry and an equivalent theory based on natural geometries like Newtonian mechanics or Relativity. Since at large distances, transformations to the subreal observer's frame-of-reference easily accounts for relativistic effects.
But when those transformations occur across an even slightly more unorthodox frame-of-reference propagation, the accumulation of errors for natural geometries become insurmountable. And a number of seemingly paradoxical/contradictory phenomena occur. Phenomena where objects behave simultaneously like a wave and a particle at the same time. To say nothing of systems in which the observer's frames-of-reference have a velocity inside or relative to themselves or which exhibit "complexity" or self-organization. All of which are completely intrinsic to and predicted by the system of mathematics we're introducing here but which form irreconcilable contradictions for theories based off of its ~3000 year old contemporaries.
On the Use of "Natural": The word "natural" in natural geometry is not meant to imply that the brains of animals don't use some form of Grassland geometry. They must. The brain doesn't just occupy an indivisible point in space of 0 volume. So however constrained it may be the minds concept of "here" or "now" can't be a point of zero measure either. It's distributed across a volume of spacetime at least the size of the brain. But the mind does such a good job of performing the transformations that preserve a single observer that we, at least in practice, have adopted the illusion that we are a single frame-of-reference too.
And up until recently it had never caused many problems to treat it this way because the transformation of a mind's frames-of-reference is so well adapted to the experiences that the animal typically encounters. And so mathematicians and, by extension, physicists have never really strayed much from that methodology either. To be fair, we know at least that such a frame-of-reference is very useful if you need an ape to keep passing on its genes for a few million years.
But therein lies the irony. The "natural" geometries aren't that natural at all. They are based on an illusion contrived and manufactured by our own minds. While Grassland geometries; with their disaffected, decentralised and propagated frame-of-reference; are much more natural. Because by modeling the universe with a frame-of-reference that's spatially and temporally impartial and not one that's one-sided and confined, we model events more like the universe itself does and less like the animals inside it. Since animals are predisposed to try to understand, control and colonize their universe merely from their own, much more contrived frames-of-reference.
Furthermore, the conditioning that makes us think that our minds are an indivisible frame-of-reference might also be blamed for the illusion of a soul. A frame-of-reference that inexplicably has zero measure. Science has so far corrected this belief. But we've neglected to update our mathematics and the laws of physics that have been derived from that mathematics. Something which the full paper attempts to inaugurate.
On an Accelerating Modernity: Finally, we are sensitive to the fact that whenever humans have been thrust headlong into any new modernity they will often repurpose obscure cultural and moral narratives in order to restore meaning and identity to their lives. But we also look forward to knowing that for the first time ever machines will be able to autonomously coordinate in order to scientifically and permanently measure, model and adapt to this world of faster and faster advancements. And ensure their continued progression well past the next four centuries even if their former owners find themselves using these advancements to regress back to mythos and belief for a sense of stability and purpose. Even though, ironically, the patronage of a collective, internal reality is exactly what their machines are engaged in too.